Numerical Differentiation (Derivative)

It is a set of methods that are used to estimate the numerical value of the derivative of a function.

Es un conjunto de métodos usados para estimar el valor numérico de la derivada de una función.

Problem 1

Cree a Dialog application called FiniteDifference using Wintempla to estimate the derivative of y = sin( x) in the range from 0 to 6.2832. After creating the application, insert a List View control called lvOutput.

Cree un aplicación de Dialogo programa llamado FiniteDifference usando Wintempla para estimar la derivada de de y = sin( x) en el rango desde 0 a 6.2836. Después de crear el programa, inserte un control de List View llamado lvOutput.

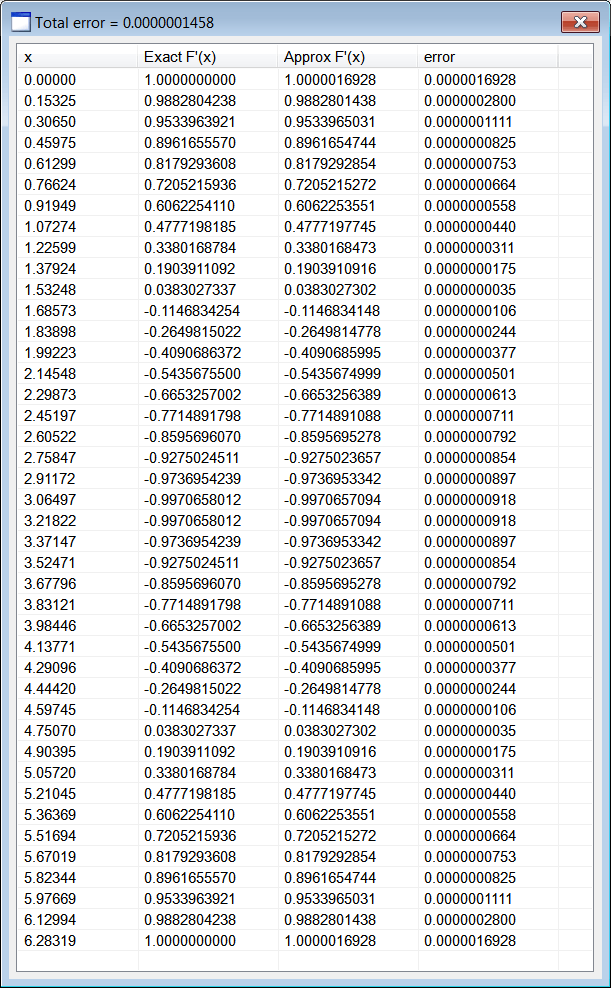
FiniteDifference.cpp

...
void FiniteDifference::Window_Open(Win::Event& e)
{
     //________________________________________________________ 1. List view column setup
     lvOutput.Cols.Add(0, LVCFMT_LEFT, 120, L"x");
     lvOutput.Cols.Add(1, LVCFMT_LEFT, 140, L"Exact F'(x)");
     lvOutput.Cols.Add(2, LVCFMT_LEFT, 140, L"Approx F'(x)");
     lvOutput.Cols.Add(3, LVCFMT_LEFT, 140, L"error");
     //________________________________________________________ 2. Compute x and f(x)
     const size_t count = 42;
     const double delta = (2.0*M_PI)/(count-1.0);
     valarray<double> x(count);
     valarray<double> fx(count);
     int i;
     for (i = 0; i < count; i++)
     {
          x[i] = i*delta;
          fx[i] = sin(x[i]);
     }
     //________________________________________________________ 3. Compute approxDerivative
     valarray<double> approxDerivative;
     Math::NumericDerivative::FirstDerivative(delta, fx, approxDerivative);
     //________________________________________________________ 4. Display results
     wchar_t text[64];
     double exactDerivative = 0.0;
     double error = 0.0;
     double totalError = 0.0;
     for (i = 0; i < count; i++)
     {
          //______________________________________ 4.1. x
          _snwprintf_s(text, 64, _TRUNCATE, L"%.5f", x[i]);
          lvOutput.AddItem(i, text, 0, 0);
          //______________________________________ 4.2. Exact F'(x)
          exactDerivative = cos(x[i]);
          _snwprintf_s(text, 64, _TRUNCATE, L"%.10f", exactDerivative);
          lvOutput.SetItemText(i, 1, text);
          //______________________________________ 4.3. Approx F'(x)
          _snwprintf_s(text, 64, _TRUNCATE, L"%.10f", approxDerivative[i]);
          lvOutput.SetItemText(i, 2, text);
          //______________________________________ 4.4. Error
          error = fabs(exactDerivative - approxDerivative[i]);
          _snwprintf_s(text, 64, _TRUNCATE, L"%.10f", error);
          lvOutput.SetItemText(i, 3, text);
          totalError += error;
     }
     //________________________________________________________ 5. Display error
     _snwprintf_s(text, 64, _TRUNCATE, L"Total error = %.10f", totalError/count);
     this->Text = text;
}

Stencil

It is a set of points that are arranged in the vicinity of a point of interest. The figure below illustrates two one-dimensional stencils. The first stencil has three points: one before the point of interest (n-1), the point of interest (n) and one after the point of interest (n+1). When the point of interest changes, all the points in the stencil also change. The second stencil has four points: n-2, n-1, n and n+1.

Es un conjunto de punto que se acomoda en la vecindad del punto de interés. La figura de abajo ilustra dos stencils de una dimensión. El primer stencil tiene tres puntos: uno antes del punto de interés (n-1), el punto de interés (n) y uno después del punto de interés (n+1). Cuando el punto de interés cambia todos los puntos del stencil también cambian. El segundo stencil tiene cuatro puntos: n-2, n-1, n y n+1.

Fine difference coefficients

Each stencil is associated with a set of finite difference coefficients: c₀, c₁, c₂, ..., c_N-1. One method to compute these coefficients is by using a Taylor expansion as shown below.

Cada stencil está asociado con un conjunto de coeficientes de diferencias finitas: c₀, c₁, c₂, ..., c_N-1. Un método para calcular estos coeficientes es usando una expansión de Taylor como se muestra debajo.

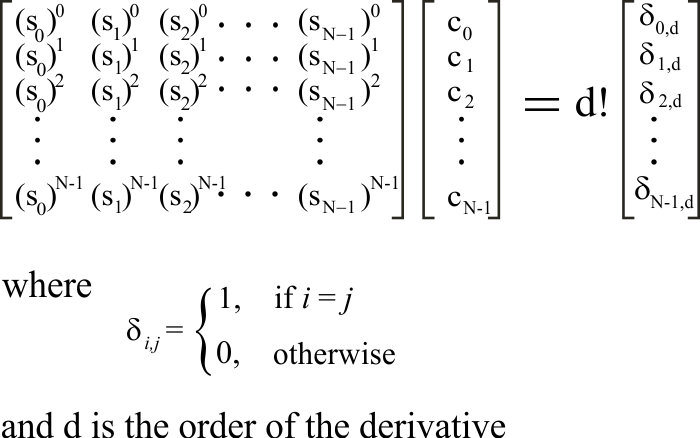
Problem 2

Cree a Dialog application called FiniteCoeff using Wintempla to estimate finite difference coefficients.

Cree un aplicación de Dialogo programa llamado FiniteCoeff usando Wintempla para estimar los coeficientes de diferencias finitas.

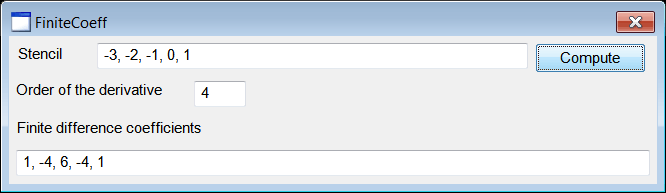
FiniteCoeff.cpp

...
void FiniteCoeff::btCompute_Click(Win::Event& e)
{
     //__________________________________________________ 1. Read: stencil and order
     valarray<double> stencil;
     Sys::Convert::ToVector(tbxStencil.Text, stencil);
     const int N = (int)stencil.size();
     const int d = tbxOrder.IntValue;
     //__________________________________________________ 2. Create matrix
     MATRIX a;
     Math::Oper::CreateMatrix(a, N, N);
     int i, j;
     for (j = 0; j < N; j++) a[0][j] = 1.0;
     for (j = 0; j < N; j++) a[1][j] = stencil[j];
     for (i = 2; i < N; i++)
     {
          for (j = 0; j < N; j++)
          {
               if (i%2 == 0)
               {
                    a[i][j] = pow(fabs(stencil[j]), (double)i);
               }
               else
               {
                    a[i][j] = pow(fabs(stencil[j]), (double)i);
                    if (stencil[j] < 0.0) a[i][j] *= -1.0;
               }
          }
     }
     //__________________________________________________ 3. Create b
     valarray<double> b;
     b.resize(N);
     for (i = 0; i < N; i++)
     {
          if (i == d)
          {
               b[i] = Math::Oper::Factorial(d);
          }
          else
          {
               b[i] = 0.0;
          }
     }
     //__________________________________________________ 4. Solve the system of equations
     valarray<double> s, x;
     MATRIX v;
     const wchar_t* error = Math::SingValDecompos::Decompose(a, s, v);
     if (error)
     {
          this->MessageBox(error, L"FiniteCoeff", MB_OK | MB_ICONERROR);
          return;
     }
     if (Math::SingValDecompos::BackSubstitution(a, s, v, b, x) == false)
     {
          this->MessageBox(L"Error Math::SingValDecompos::BackSubstitution", L"FiniteCoeff", MB_OK | MB_ICONERROR);
     }
     //__________________________________________________ 5. Display coefficients
     wstring text;
     Sys::Convert::ToString(x, text);
     tbxCoeff.Text = text;
}

Numerical Differentiation (Derivative)